Способы измерения площади геометрия

Основные способы

Существует три основных способа определения площадей:

При использовании аналитического способа определение площади производится по результатам полевых угловых и линейных измерений (или координат) характерных точек.

Для графического способа используются данные измерений на плане и карте.

Такой способ чаще всего используется при отсутствии информации полевых измерений.

При механическом способе площадь определяется по плану с помощью специального устройства – планиметра.

Иногда используется комбинированный способ определения площади. Например, общая площадь участка определяется по координатам характерных точек аналитическим способом, а площади внутренних участков определяются по плану с помощью графического или механического методов.

Эти три метода имеют различные показатели точности.

Точности других методов, использующих топографическую информацию с планов, зависят еще и от погрешностей приборов, качества плана, масштаба, деформации бумаги.

Аналитический способ

Аналитический способ позволяет по координатам характерных точек границ участка определить его площадь. При этом используются формулы аналитической геометрии.

В соответствии с ними площадь многоугольника S может быть определена по формуле:

• Xi и Yi – координаты i-той характерной точки участка, имеющего вид многоугольника;
• i – порядковый номер характерной точки ЗУ. Этот параметр меняется от 1 до n;
• n – число характерных точек.

Если участок имеет четырехугольную форму, то, в общем случае, для него расчет площади производится по приведенной выше формуле с учетом того, что n=4.

Если участок имеет форму трапеции и известны его стороны, то площадь такого участка можно определить по формуле:

• a и b – основания фигуры;
• h – высота трапеции.

При расчете четырехугольника неправильной формы, когда известны размеры его сторон, вначале определяют величину полупериметра p:

a,b,c,d – величины сторон.

Тогда площадь участка Sу будет равна:

При этом по контуру границ участка производится замер азимута каждой характерной точки. Также определяется расстояние от одной характерной точки до следующей за ней точки. Вся эта информация в дальнейшем вводится в ЭВМ, которая по специальной программе производит расчет площади ЗУ.

Графический метод

При расчете площади участка графическим методом чаще всего изображенный на плане участок сложной формы делят на участки элементарного вида (треугольники, прямоугольники, трапеции), затем вычисляют и суммируют площади этих фигур.

Точность графического метода зависит от точности графического измерения на плане. Известно, что точность измерения с помощью циркуля постоянна и равна 0,1 мм. Поэтому относительная ошибка при измерении коротких линий больше, чем при измерении длинных линий. В связи с этим желательно, чтобы простые фигуры были больших размеров и с близкими по размерам основаниями и высотами.

Такой метод удобен в случае, когда имеется небольшое количество характерных точек. В противном случае целесообразнее определять площадь участка по координатам точек, измеренных на плане.

Палетка представляет собой прозрачный лист, на который нанесены деления. Этот лист накладывается на план участка. Сосчитав количество делений, входящих в контур участка, и определив площадь одного деления с учетом масштаба, можно оценить площадь участка.

Сближение меридианов. Переход от геодезического азимута к дирекционному углу.

Сближение меридианов y — это угол в данной точке между ее меридианом и линией, параллельной оси абсцисс или осевому меридиану.

Направлению геодезического меридиана на топографической карте соответствуют боковые стороны ее рамки, а также прямые линии, которые можно провести между одноименными минутными делениями долгот.

Счет сближения меридианов ведется от геодезического меридиана. Сближение меридианов считается положительным, если северное направление оси абсцисс отклонено к востоку от геодезического меридиана и отрицательным, если это направление отклонено к западу.

Величина сближения меридианов, указанная на топографической карте в левом нижнем углу, относится к центру листа карты.

При необходимости величину сближения меридианов можно вычислить по формуле

y=(L — L 4) sin B,

где L — долгота данной точки;

L 4— долгота осевого меридиана зоны, в которой расположена точка;

B — широта данной точки.

Широту и долготу точки определяют по карте с точностью до 30`, а долготу осевого меридиана зоны рассчитывают по формуле

L 4= 4  06 5  0N — 3 5,

где N — номер зоны

Пример. Определить сближение меридианов для точки с координатами:

B = 67 5о 040` и L = 31 5о 012`

31 5о 012`

Решение. Номер зоны     N = ______ + 1 = 6;

6 5о

L 4o  0= 4  06 5о 0 * 6 — 3 5о 0 = 33 5о 0;  y = (31 5о 012` — 33 5о 0) sin 67 5о 040` =

-1 5о 048` * 0,9245 = -1 5о 040`.

Сближение меридианов равно нулю, если точка находится на осевом меридиане зоны или на экваторе. Для любой точки в пределах одной координатной шестиградусной зоны сближение меридианов по абсолютной величине не превышает 3 5о 0.

Геодезический азимут направления отличается от дирекционного угла на величину сближения меридианов. Зависимость между ними может быть выражена формулой

A = a + (+ y)

Из формулы легко найти выражение для определения дирекционного угла по известным значениям геодезического азимута и сближения меридианов:

a = А — (+ y).

Как без труда рассчитать площадь участка сложного контура

Большинство зарегистрированных земельных участков (ЗУ) имеют установленные границы, которые определяются межевыми знаками, природными урочищами и искусственными объектами.

Проводить межевание земельных наделов необходимо, чтобы отделить участок от соседних ЗУ, общественных территорий, а также зон сервитута. По границам можно определить контур участка и рассчитать его площадь.

Площадь является важной характеристикой земельного участка:

• по ней устанавливается его кадастровая или рыночная стоимость;
• производится планировка;
• устанавливается земельный налог.

Если контур ЗУ представляет собой правильный прямоугольник, то рассчитать его площадь не представляет сложности: для этого достаточно длину стороны, А умножить на длину стороны В. Но гораздо чаще очертания ЗУ имеют неправильную форму, и тогда для расчета лучше использовать калькулятор площади земельного участка.

Калькулятор площади земельного участка

Этот калькулятор крайне прост в использовании — нужно просто измерить стороны А, В, С и D и вставить значения в калькулятор.

Если ЗУ имеет правильную прямоугольную форму, сторона, А принимается равной D, а B — С. Например, чтобы рассчитать площадь земельного надела длиной 103 м, шириной 57 м, нужно заполнить поля в следующей последовательности: А — 103 м, В — 57 м, С — 57 м, D — 103 м.

Расчет площади участка сложного контура

Если контур земельного участка — это сложная фигура, то ее можно разбить на две и более фигур.

Например, пятиугольник на рисунке ниже состоит из треугольника EFC и четырехугольника ABCD. Площадь четырехугольника S рассчитывается уже известным нам способом. Что касается площади треугольника, то она равна половине площади четырехугольника EHFJ, в том случае если один из углов треугольника равен 90 градусов (прямоугольный треугольник).

Зададим длины сторон сложного контура ЗУ: А = 80 м; В = 70 м; С = 75 м; D = 60 м; E = 60 м; F = 50 м.

• Вначале рассчитаем площадь фигуры ABCD, подставив в калькулятор значения сторон А, В, С и D: Sabcd = 5023 м2.
• Теперь определим S фигуры EHFJ, подставив в качестве, А и D — Е (60), В и С — F (50): Sehfi = 3000 м2.
• Площадь треугольника EFC: Sefc = 3000/2 = 1500 м2.
• S земельного участка: 5023 + 1500 = 6023 м2.

Однако если треугольник не прямоугольный, расчет Sefc следует производить по другим формулам, в частности, как половину произведения высоты треугольника h на его основание C.

Например, если h равна 45 м, а С — 75 м, то Sefc будет равна ½×45×75 = 1687 м2.

Sзу = 5023 + 1687 = 6710 м2.

Практическое применение калькулятора

Знание площади ЗУ позволяет определить величину земельного налога. Например, известны:

• средняя кадастровая стоимость одного метра земли в регионе — 5000 руб/м2;
• размеры участка А, В, С и D — 40, 30, 35 и 20 м2 соответственно;
• расположение надела в жилой зоне, то есть ставка налогообложения — 1,5%.

Площадь, рассчитанная по калькулятору площади ЗУ — 924,47 м2 или 9,24 сотки.

Дальнейший расчет:

• Кадастровая стоимость: КС = 5000×924,47 = 4 622 350 руб.
• Величина земельного налога ЗН = 1,5% х 4 622 350 = 69 335 руб.

Эту сумму необходимо будет выплачивать ежегодно.

Использовать калькулятор следует для ориентировочной оценки стоимости земельного надела и имущественного налога, если участок новый и еще не поставлен на кадастровый учет. Если ЗУ зарегистрирован в ЕГРН, узнать его точную стоимость и площадь можно на сайте Росреестра, введя в поле поисковой формы кадастровый номер или адрес участка.

Другой вариант — воспользоваться земельным калькулятором в виде карты, который даст результат только в том случае, если ЗУ есть в базе данных.

От чего зависит кадастровая стоимость и налог

Величина кадастровой стоимости земли зависит от многих факторов:

• региона;
• географического положения участка;
• назначения земли и т. д.

Земельные наделы в землях под ведение фермерского хозяйства, ЛПХ, сельскохозяйственной деятельности могут быть намного дешевле ЗУ под ИЖС.

На величину налога оказывают влияние:

• налоговая ставка, которая может быть разной в различных регионах;
• наличие льгот (все категории льготников перечислены в ст. 391 НК РФ).

Межевание земли

Чтобы определить точные границы участка, необходимо провести межевание, которое отделит земельный надел от соседних частных участков и территории публичного пользования.

• Надо вызвать кадастрового специалиста, который проведет геодезические съемки, привяжет данный надел к единым государственным координатам, а в точках поворотах контура установит межевые знаки.
• После того как межи установлены, можно смело приступать к замеру длин сторон и расчету площади, а также планировке строительных работ.

Калькулятор площади земельного участка

Загрузка…

Расчет площади земельного участка

Наиболее точно рассчитать площадь участка земли можно аналитическим методом. Точность такого метода определена тем, что на него влияют только ошибки полевых измерений. Для участков простой формы используются простые формулы геометрии.

Для участков с более сложной формой расчеты производятся по координатам поворотных точек, а для сверх сложных участков используются программы, исходными данными для которых являются углы азимута точек.

Определение площади

Существует несколько способов такого определения площади участков земли:

Если вы хотите узнать, как в 2019 году решить именно Вашу проблему, обращайтесь через форму онлайн-консультанта или звоните по телефонам:

• Москва: +7 (499) 110-86-72.
• Санкт-Петербург: +7 (812) 245-61-57.

• аналитический;
• графический;
• механический.

Наиболее точным из этих методов является аналитический. Это связано с тем, что при его использовании на точность результатов влияют только ошибки полевых измерений, тогда как на два других метода оказывают влияние ошибки плана или карты, с которых снимаются данные.

Расчет площади аналитическим методом

При использовании аналитического способа площадь определяется по данным полевых измерений или по координатам поворотных точек, являющихся функциями результатов полевых измерений.

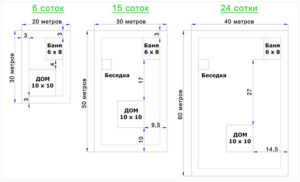
Участки имеют разные геометрические формы. В частности, они могут иметь четырехугольную форму.

Такая форма участка часто существует в старых садоводческих товариществах, в которых нарезались участки в 6 соток.

Если участок имеет форму трапеции и известны основные параметры такой фигуры, то площадь участка может быть рассчитана по формуле:

Если вы хотите узнать, как решить именно Вашу проблему, обращайтесь через форму онлайн-консультанта или звоните по телефонам:

• Москва: +7 (499) 110-86-72.
• Санкт-Петербург: +7 (812) 245-61-57.

• a и b – основания фигуры;
• h – высота трапеции.

Если известны координаты поворотных точек , то площадь надела может быть определена по приведенной ниже общей формуле для многоугольника. При этом для трапеции расчет площади производится по формуле с учетом того, что n=4.

При расчете четырехугольника неправильной формы, когда известны величины каждой из его сторон, необходимо определить величину периметра 2p:

2р=(а+b+c+d), где:

a,b,c,d – величины сторон.

Тогда площадь участка Sнф будет равна:

Sнф=√(p-a)(p-b)(p-c)(p-d).

В формуле используется значение половины периметра p.

Если участок имеет форму многоугольника с n сторонами, то его площадь рассчитывается по координатам поворотных точек:

Sу= 0,5*∑(Xi*(Yi+1-Yi-1), где:

• Xi и Yi – координаты i-той поворотной точки участка, имеющего вид многоугольника;
• i – порядковый номер точки. Этот параметр меняется от 1 до n;
• n – число характерных точек.

Для проверки правильности расчетов используется другая формула:

Sу1= 0,5*∑(Yi*(Xi+1-Xi-1).

Если расчеты проведены правильно, то Sу1 = Sу.

При наличии участка сложной формы со многими точками поворота расчет по приведенным выше формулам может стать затруднительным.

В этом случае аналитический расчет площади участка производится с использованием данных об углах азимута.

При этом по контуру границ участка производится замер азимута каждой поворотной точки. Также определяется расстояние от одной точки до следующей за ней точки.

Вся эта информация в дальнейшем вводится в ЭВМ, которая по специальной программе производит расчет площади земельного надела.

Точность расчетов площади

При определении площади участка необходимо учитывать погрешности расчета площади.

В частности, если площадь участка рассчитана по координатам поворотных точек, то разница между расчетным и зафиксированным в ЕГРН значениями площади ЗУ не должна быть больше допустимой величины (dSдоп).

В нормативных документах эта величина определена следующим образом:

dSдоп=3,5*Mt*√Sу где:

• Mt – погрешность (СКП) расположения поворотной точки;
• Sy-площадь участка.

При этом если dS превышает допустимую величину, то необходимо провести проверку точности координат и методики расчета площади участка.

Если же dS оказывается меньше допустимого значения, то за окончательное значение площади может быть принято расчетное значение площади с указанием допустимого значения dPдоп.

Пример.

Вычисленная площадь участка № 103 снт “Изобретатель” составила 594 кв. м. По документам площадь участка равна 600 кв. м.

СКП Мt при межевании для садоводческих товариществ определена нормативно (приказ МЭР №518) и равна 20 см. Тогда:

dS = 600-594= 6 кв. м

dSдоп=3,5*0,2* √600=17,14 кв. м

Окончательное значение площади участка №103 Sy=594±17 кв. м.

• Москва: +7 (499) 110-86-72.
• Санкт-Петербург: +7 (812) 245-61-57.

Площадь фигуры, ее основные свойства. Способы измерения площадей фигур. Единицы площади

1. Площадь фигуры.

2. Способы измерения площади фигуры.

3. Равновеликие и равносоставленные фигуры.

4. Единицы площади. Отношения между ними.

5. Измерение площадей простейших фигур.

6. Измерение площадей фигур в начальной школе.

Рассмотрим вопрос о площади плоской фигуры и способах измерения площадей.

Дадим аксиоматическое определение площади, согласно и аксиоматическим определениям темы 1.

Функцией площади называется любая функция S : U R_>0, обладающая свойствами:

1) конечной аддитивности, т.е. » u, v Є u,

2) Gs — инвариантности, т.е. «u Є U, » g Є (L₂ х R 2 ),

Рассмотрим основы теории измерения площадей плоских фигур, взяв за основу подход, впервые изложенный французским математиком К. Жорданом согласно.

Пусть М — множество фигур на плоскости, имеющих замкнутых контур, и Ф — одна из таких фигур, площадь которой надо измерить. По отношению к фигуре Ф будем различать внутренние и внешние точки, а так же точки контура. Далее, через производную точку плоскости проведем две взаимно перпендикулярные прямые (оси) и выберем единичный отрезок l. Откладывая на каждой прямой единичный отрезки, равные единичному, и проведя через их концы прямые, параллельные осям, получим на плоскости сеть квадратов (рис. 1), площадь каждого из которых равна единице.

Заштрихуем те квадраты, через которые проходит контур фигуры Ф. Тогда по отношению к фигуре Ф выделяются квадраты трех видов:

1) квадраты, целиком состоящие из внутренних точек фигуры Ф;

2) квадраты, состоящие как из внутренних, так и внешних точек фигуры (на рис. 1 они заштрихованы);

3) квадраты, не содержащие внутренних точек фигуры Ф.

покрывающей

Система квадратов, состоящая из всех квадратов первого вида, называется внутренней системой квадратов по отношению к фигуре Ф.

Численные значения площадей внутренней и покрывающей систем квадратов легко подсчитать. Если рассматривать только единичные квадраты, то эти значения выражаются натуральными числами m₁ и n₁ соответственно. Здесь m₁ — число единичных квадратов, целиком лежащих внутри фигуры Ф, а n₁ — число единичных квадратов покрывающей системы для фигуры Ф. Таким образом, m₁ и n₁ будут приближенными значениями измеряемой площади: первое m₁ — с недостатком; второе n₁ — с избытком.

Разделим каждую из сторон единичного квадрата на 10 равных частей и проведем через точки деления прямые, параллельные сторонам квадрата. При этом единичный квадрат разложится на 100 равных квадратов. Пользуясь новым квадратом, образуем на плоскости более мелкую сеть. Обозначим через m₂ и n₂ число новых квадратов внутренней и покрывающей систем, соответственно. Тогда числа

Деля каждую из сторон малых квадратов снова на 10 равных частей, образуем еще более мелкую сеть. При этом числа

Кроме того, для любого j > 1 имеем:

Из соотношения

Способы определения площадей

Методы определения площадей.

Способы определения площадей.

Составление различного рода проектов, связанных с использованием земельной территории для строительства, изучение её природных богатств, учет земель требуют определения площадей.

При проведении землеустроительных и кадастровых работ определяют как небольшие площади усадебных и садовых участков, полей севооборотов, контуров сельскохозяйственных угодий и др. так и большие площади- городских и сельских населенных пунктов, целых землепользований, лесных массивов, нескольких несмежных участков, обладающих одними и теми же природными или хозяйственными признаками, например, суммы площадей контуров пашни, кормовых угодий и др.

В одних случаях достаточно ограничиться общими сведениями о площадях участков и массивов, в других -необходимы более точные определения площадей и погрешность даже в несколько десятых долей процента считается недопустимой.

В зависимости от хозяйственной значимости участков и массивов, их размеров, конфигурации и вытянутости, наличия результатов измерений линий, углов на местности и планово-картографического материала, топографических условий местности применяются следующие способы определения площадей:

• Аналитический, когда площадь вычисляют по результатам измерений линий и углов на местности или по их функциям-координатам вершин фигур.
• Графический, когда площадь вычисляют по результатам измерений линий и углов (транспортиром) или по координатам точек на плане (карте).
• Механический, когда площади определяют на плане при помощи специальных приборов (планиметров) и приспособлений (палеток, ротометров и др.).

Нередко эти способы применяют комбинированно, например, часть линейных величин для вычисления площади измеряют на плане, а часть берут из результатов измерений на местности, или при вычислении площади по координатам для одних точек принимают вычисленные (аналитические) значения координат по результатам измерений на местности, а для других точек координаты получают измерением на плане (графические), или основную площадь земле­пользования, заключенную в теодолитный полигон, вычисляют анали тическим способом, а площадь, выходящую за пределы полигона и заключенную между линиями полигона и живым урочищем (границей землепользования по ручью, берегу реки и др.), определяют графическим и механическим способом.

Наиболее точным, но требующим больших материальных затрат на производство полевых измерений, является аналитический способ, так как на точность вычисленной площади этим способом влияют только погрешности измерений на местности, и, следовательно, точность его не зависит от точности плана. Его применяют для вычисления площадей населенных пунктов, усадебных и садовых участков, землепользований, когда по границам их проложены теодолитные ходы и полигоны, а также при обмере ценных в хозяйственном отношении других участков.

Менее точен графический способ, потому что, помимо погрешностей измерений на местности на точность вычисленной площади влияют погрешности составления плана и определения площади по плану. Его применяют для определения площадей полей и контуров угодий, ограниченных ломаными линиями, при этом, чем меньше площадь участка, тем с большей относительной погрешностью определяется его площадь.

Наименее точным является механический способ, так как пользуясь им, можно быстро и просто определить площадь участка любой формы, поэтому его применяют при определении площадей контуров угодий с извилистой формой границ, проходящих по живым урочищам, бровкам лощин, очертаниям болот, зарослей и пр.

Источник

Измерение площади лекал

Нормирование расхода материалов

Сущностью нормирования является установление рациональной нормы расхода материала на единицу изделия путём разработки рациональной раскладки.

Норма расхода материала – максимально допустимая величина расхода материала для изготовления единицы изделия, установленного уровня качества.

Нормированию подлежат все виды материалов и фурнитуры

Структура нормы состоит из:

1 Полезная площадь лекал с учётом вытачек, но без учета площади припусков на швы надставок и припусков на подгонку рисунка ткани.

2 Технологические потери: межлекальные потери, потери, по ширине учитывая потери от кромки, потери по длине, учитывают потери слабины при настиле, на стык, на равноту конца настила и конечный остаток.

Существует два вида норм:

Индивидуальная – разработанная на единицу изделия для расчета: нормы на раскладку, нормы на настил, нормы расхода ткани на единицу изделия.

Групповая – разработанная на основе лучшей раскладки, применятся для планирования объема продукции.

Очень важным в точном установлении норм является точное измерение площади самих лекал. Существует ряд способов измерения площади лекал. Отмечаем четыре из них.

Геометрический – площадь каждого лекала разбивают на простейшие геометрические фигуры, суммируют их и получают площадь лекал. Погрешность составляет 2–3 %.

Комбинированный (палетка) – заключается в том, что из площади полного прямоугольника, в который вписывается лекало, вычитывают сумму площадей прямоугольников не входящих в форму лекала.

Механизированный – выполняется на машине ИЛ. Она оснащена чувствительным фотоэлементом, её работа основана на базе контактных измерений площади плоских фигур, разной конфигурации путем разложения их на элементы оптической площади.

Способ взвешивания. Лекала раскладывают произвольно на листе бумаге, очерчивают контуры и замеряют площадь прямоугольника, в который вписываются все лекала. Затем прямоугольник отрезают и взвешивают, отдельно вырезают каждое лекало и взвешивают. Дальнейший расчет площади происходит по формуле 6.1:

S_{р –} площадь прямоугольника, см 2 ,

М_р— масса прямоугольника, г

Площади лекал для проектируемой модели представлены в таблице 12.

Таблица 13– Площади лекал. Женское платье спортивного стиля. Размер 164-92-100, вторая полнотная группа, младшая возрастная группа.

Наименование деталей изделия и материалов	Количество единиц, ед.	Площадь, м 2
Лекал	Деталей кроя	Лекал	Деталей кроя
1	2	3	4	5
Основная ткань Трикотажное полотно
1 Середина переда	1	1	0,154224	0,154224
2 Боковая верхняя часть переда	1	2	0,05904	0,11808
3 Боковая нижняя часть переда	1	2	0,054064	0,108128
4 Середина спинки	1	1	0,15808	0,15808
5 Боковая часть спинки	1	2	0,12832	0,25664
6 Рукав	1	2	0,049632	0,099264
7 Воротник	1	1	0,123136	0,123136
8 Обтачка переда	1	1	0,01408	0,01408
9 Обтачка спинки	1	2	0,0064	0,0128
Итого :	9	14	0,746976	1,044432

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Площадь фигуры, её свойства. Способы измерения площадей фигур. Единицы площади. Вычисление площадей квадрата, прямоугольника, треугольника, круга, трапеции.

Первое представление о площадях – в дошк. возрасте (н-р: сравнивая платочки).Геометр фигура плоская, если все точки принадлежат 1 плоскости. S фигуры – положит величина, определяется для каждой фигуры, так что: 1) равные фигуры имеют = S; 2) S фигуры = сумме S всех ее компонентов. Равные фигуры – совпадают при наложении. Равновеликие – S равны. Равносоставленные – две фигуры, которые можно разбить на соответ равные части (только многоугольники). Теорема Бойян и Гервина: 1) равносоставленные фигуры = равновеликие; 2) если у 2 многоугольников S =, то их можно представить из 2 попрано = частей.

Св-ва S: 1)если фигуры =, то = их числ значения S; 2) если фигура состоит из частей, то S = сумме S этих частей; 3) при замене ед S, числ значение S увеличивается во столько раз, во сколько ед S; 4) числ значение S единичного квадрата = 1; 5) если F₁ – часть F₂, то численное значение F₁ 2 2 . Чтобы найти приближенное значение S_(F) достаточно сложить получ числовые значения S по недостатку и по избытку :2. S_(F)

(me+(m+n)e 2 )/2 = ((m+n+m)e 2 )/2= (2m/2 +n/2)e 2 = (m+n/2)e 2 . Для более точно значения – более мелкая палетка, или наклонить с разных углов, и высчитать среднее арифметическое.

Ед S. м 2 , см 2 , дм 2 , км 2 , мм 2 , ар, га, сотка.

Формулы площади квадрата

1) Формула площади квадрата по длине стороны

Площадь квадрата равна квадрату длины его стороны. S = a2

2) Формула площади квадрата по длине диагонали

Площадь квадрата равна половине квадрата длины его диагонали.

где S — Площадь квадрата, a — длина стороны квадрата, d — длина диагонали квадрата.

Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон

S = a · b, где S — Площадь прямоугольника, a, b — длины сторон прямоугольника.

Формулы площади треугольника

1) Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты. S = 1 a · h

2) Формула площади треугольника по трем сторонам

Формула Герона: S = √p(p — a)(p — b)(p — c)

3) Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними. S = 1 a · b · sin γ

4) Формула площади треугольника по трем сторонам и радиусу описанной окружности.

5) Формула площади треугольника по трем сторонам и радиусу вписанной окружности

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. S = p · r, где S — площадь треугольника, a, b, c — длины сторон треугольника, h — высота треугольника, γ — угол между сторонами a и b, r — радиус вписанной окружности, R — радиус описанной окружности,

p = a + b + c — полупериметр треугольника.

Формулы площади круга

1) Формула площади круга через радиус

Площадь круга равна произведению квадрата радиуса на число пи. S = π r2

2) Формула площади круга через диаметр

Площадь круга равна четверти произведения квадрата диаметра на число пи. S = 1 π d2

где S — Площадь круга, r — длина радиуса круга, d — длина диаметра круга.

Формулы площади трапеции

1) Формула Герона для трапеции

S = a + b √(p — a)(p — b)(p — a — c)(p — a — d)

2) Формула площади трапеции по длине основ и высоте

Площадь трапеции равна произведению полусуммы ее оснований на высоту.

где S — площадь трапеции,a, b — длины основ трапеции, c, d — длины боковых сторон трапеции, p = a + b + c + d — полупериметр трапеции.

Источник