Площадь пятиугольника онлайн калькулятор по сторонам

Содержание:

Для расчета площадь пятиугольника для начала нам нужно определить, регулярно это или нет. Пятиугольник — это многоугольник, замкнутая плоская фигура с пятью сторонами. Когда многоугольник правильный, это означает, что длина его сторон одинакова, а его внутренние углы одинаковы.

В этом случае есть формула для вычисления точной площади правильного многоугольника, зная некоторые из его основных характеристик, которые мы выведем позже.

Если многоугольник не правильный, то есть имеет стороны разных размеров и неравные внутренние углы, единой формулы не существует.

Однако математики нашли методы вычислений, такие как разделение фигуры на другие с меньшим количеством сторон, такие как треугольники, квадраты и прямоугольники, размеры которых легко узнать или вычислить.

Еще одна процедура для вычисления площадей полигонов в целом, зная координаты их вершин, — это метод, называемый Гауссовские детерминанты, о котором мы расскажем позже.

Определение площади сложной фигуры с помощью теории вероятностей

Да мало ли зачем. Например, возникла необходимость определить площадь территории на карте.

Конечно, можно посмотреть в справочнике или поискать в интернете, но иногда и территории бывают нестандартными — допустим, вы озаботились проблемами лесов в пойме Амазонки и хотите ежемесячно измерять площадь зелёных пятен на фотографиях со спутника.

Если вы ботаник (в хорошем смысле слова), то вам может понадобиться измерить площадь листовой поверхности разных сортов одного растения. Или, к примеру, более прозаичная задача — нужно зашпатлевать кусок стены, а банки шпатлёвки хватает только на 1 кв. м. — нужно выяснить, покупать одну банку или раскошелиться на две.

В чём сложность нахождения площади?

Конечно, если фигура представляет собой прямоугольник, круг или, что хуже, эллипс, то проблема решается с помощью Google и калькулятора. Но где бы найти формулу, да попроще, для нахождения площади, скажем, такого рисунка?

Теория вероятностей, Ваш выход!

Сразу оговорюсь, что теория вероятностей по своей сути не подразумевает точного решения задач. Так будет и в этом случае — если вам нужна космическая точность, то предлагаю копать в сторону методов имитационного моделирования. Если же погрешность в пределах 2-5% вас вполне устраивает, то будет достаточно того же калькулятора, базовых навыков программирования и умения считать до ста.

Суть метода

Суть метода проста до банальности. Допустим, мы пасмурным деньком выложили капустный листочек (см. ремарку про биолога выше) на прямоугольный поддон, а поддон выставили под накрапывающий дождик.

А потом засекли определённое время (к примеру, пять минут) и посчитали, сколько капелек упало на поддон, а сколько непосредственно на лист.

Если принять во внимание, что дождь обычно капает равномерно, то получается простая пропорция — лист во столько раз меньше поддона, во сколько раз на него упало меньше капель дождя, чем на весь поддон

Возвращаемся к нашей фигуре

Итак, как же определить площадь той розовой пятерни? Да очень просто — заключить фигуру в прямоугольные границы и проставить случайным образом много точек. Чем больше, тем лучше (в соответствии с законом больших чисел). А потом подсчитать количество точек, попавших на фигуру.

Я намеренно не обсуждаю вопросы реализации такого алгоритма, потому что вариантов масса. Можно просто закрыть глаза и наугад тыкать шариковой ручкой, а можно действовать более научно — с помощью языков программирования.

Например, код на PHP занял у меня не больше 15 строчек, а в результате получилось вот что: Точки общим числом 300, разумеется, проставлены с помощью генератора случайных чисел.

Для удобства подсчета точек я разбил изображение на 36 секторов — теперь нужно подсчитать количество точек, попавших на изображение, в каждом секторе, а результаты сложить.

Сведём данные в таблицу (ячейка таблицы соответствует сектору на картинке):

4	8	4
7	5	6	4
3	6	13	7	8	5
1	10	10	13	7	2
2	3	7	10	2
2	5	3

Теперь у нас есть все данные для того, чтобы вычислить площадь розовой пятерни: площадь описанного прямоугольника — 20 см х 20 см = 400 кв. см; количество точек в прямоугольнике — 300; количество точек внутри фигуры (сумма значений из таблицы) — 157;

площадь фигуры – 209,33 кв. см.

И насколько это точно?

Действительно, осталось определиться с точностью данного метода. Конечно, всё зависит от количества точек, и здесь нужно соблюдать золотую середину — десяти для нашего примера было бы явно недостаточно, а от тысячи слишком рябило бы в глазах. Поэтому попробуем определить погрешность для трёхсот точек и описанного квадрата со стороной 20 см.

Для этого возьмём фигуру, площадь которой нам известна заранее.

Например, такую: Проставляем точки: Результаты заносим в таблицу:

6	11	8	5
9	15	8	5	13	2
11	8	5	14	13	5
10	11	8	8	4	4
2	14	9	10	4	1
3	5	6

Рассчитываем площадь фигуры: площадь описанного прямоугольника — 20 см х 20 см = 400 кв. см; количество точек в прямоугольнике — 300; количество точек внутри фигуры (сумма значений из таблицы) — 237;

площадь фигуры – 316 кв. см.

Нетрудно посчитать, что реальная площадь круга с радиусом 10 см составляет 314,16 кв. см. Таким образом, погрешность метода составила 0,59%, чего в большинстве случаев достаточно для прикладного использования.

• теория вероятностей
• площадь фигуры

Хабы:

Многоугольники в реальности

Невыпуклые многоугольники практически не распространены в реальной жизни: они довольно редко встречаются в природе, а в рукотворном виде она выступают в роли граней деталей машин. Многие морские организмы обладают пентасимметрией, и наиболее очевидным примером невыпуклой фигуры является морская звезда.

Правильные геометрические фигуры наоборот широко встречаются в природе. Наиболее очевидным примером являются пчелиные соты, каждая ячейка которых представляет собой гексагон. Такие гексагональные ячейки позволяют маленьким труженицам наиболее экономно использовать площадь улья, заполняя пространство без просветов. Кроме того, многие простейшие организмы, например радиолярии, имеют форму правильных полигонов.

Примеры из жизни

Пчелиные соты

Пчелиные соты — уникальный природный объект, который состоит из множества гексагональных призматических ячеек. Давайте подсчитаем, сколько таких шестиугольников находится в одних сотах. Для этого нам нужно узнать общую площадь и площадь одной ячейки. Из Википедии мы знаем, что стандартная рамка для сот имеет размеры 435 х 300 мм, соответственно, общая площадь составляет 130 500 квадратных миллиметров. Там же указано, что горизонтальный диаметр одной ячейки составляет примерно 5,5 мм. Горизонтальный диаметр полигона — это диаметр вписанной в него окружности, следовательно, мы знаем параметр r = 2,75 мм. Таким образом, при n = 6 площадь одной ячейки составляет:

Теперь мы можем узнать общее количество ячеек в одних сотах, которое выражается как 130500/26,19 = 4982

Снежинка

Снежинки имеют форму правильного треугольника или шестиугольника благодаря тому факту, что вода состоит из трех атомов и при переходе из одного агрегатного состояния в другое, молекулы воды соединяются с другими частицами и образуют треугольник или гексагон. Равносторонний треугольник — это такой же правильный полигон, как и другие, ведь он имеет три равных стороны и три равных угла. Соответственно, мы можем определить площадь такой снежинки, зная только длину стороны. Пусть сторона снежинки равна 8 условным единицам. Тогда для определения площади нам потребуется указать n = 3 и a = 8. Мы получим результат в виде:

Кроме площади абстрактной снежинки, наш калькулятор посчитал также радиусы вписанной и описанной окружности.

Совет по решению задачи, для которой многоугольник изображен на бумаге в клетку

Чаще всего озадачивает то, что в данных имеется только размер клеточки. Но оказывается, что больше сведений не нужно. Рекомендацией к решению такой задачи является разбивание фигуры на множество треугольников и прямоугольников. Их площади довольно просто сосчитать по длинам сторон, которые потом легко сложить.

Но часто есть более простой подход. Он заключается в том, чтобы дорисовать фигуру до прямоугольника и вычислить значение его площади. Потом сосчитать площади тех элементов, которые оказались лишними. Вычесть их из общего значения. Этот вариант порой предполагает несколько меньшее число действий.

Инструкция

Внимательно прочитайте условие поставленной задачи. Руководствуясь им, нарисуйте на листе бумаги предполагаемый пятиугольник.

Обозначьте длину каждой из его сторон.

Проведите в пятиугольнике две диагонали. Обозначьте длину каждой диагонали.

Обратите внимание на то, что получилось в результате проведения диагоналей, и вы увидите, что они разбивают пятиугольник на три различных между собой треугольника. Из вершины каждого треугольника проведите высоту к его основанию

Из вершины каждого треугольника проведите высоту к его основанию.

Измерьте длину высоты опущенной на основание для каждого треугольника.

Определите всех трех треугольников по формуле, приведенной ниже:S = 1/2 x H x a,где S – вычисляемая площадь
треугольника;H – высота каждого треугольника;a – длина основания треугольника.

Вычислите площадь
пятиугольника
, сложив площади этих трех треугольников.

Обратите внимание

Помните, что правильным считается тот пятиугольник, у которого и все стороны, и все углы равны между собой. Если хотя бы одна сторона или угол отличается от других, то пятиугольник не считается правильным, и его площадь нельзя рассчитывать по упрощенной схеме.

Полезный совет

Проще всего определить площадь правильного пятиугольника. Для этого достаточно просто вычислить площадь одного из треугольников, а затем умножить ее на их количество. Ведь диагонали в правильном пятиугольнике разбивают его на треугольники одинаковой площади. Значительно упрощается задача и в том случае, если два угла пятиугольника являются прямыми. Достаточно провести одну диагональ, которая разобьет пятиугольник на треугольник и прямоугольник, площади которых можно найти совсем просто. Сумма вычисленных площадей будет равна площади самого пятиугольника.

Многоугольник или полигон — геометрическая фигура, которая имеет n-ное количество углов. В общем случае многоугольник — это часть плоскости, которая ограничена замкнутой ломанной.

Свойства правильного восьмиугольника:

1. Все стороны правильного восьмиугольника равны между собой.

a₁ = a₂ = a₃ = a₄= a₅ = a₆ = a₇ = a₈.

2. Все углы равны между собой и составляют 135°.

α₁ = α₂ = α₃ = α₄ = α₅ = α₆ = α₇ = α₈ = 135°.

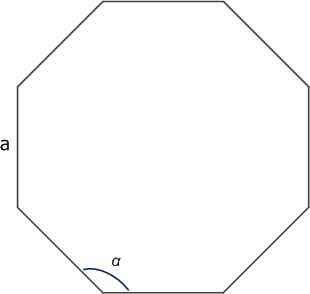
Рис. 4. Правильный восьмиугольник

3. Сумма внутренних углов любого правильного восьмиугольника равна 1035°.

4. Все биссектрисы углов между сторонами равны и проходят через центр правильного восьмиугольника O.

Рис. 5. Правильный восьмиугольник

5. Количество диагоналей правильного восьмиугольника равно 20.

Рис. 6. Правильный восьмиугольник

6. Центр вписанной окружности O₁ совпадает с центром описанной окружности O₂, что и образуют центр многоугольника O.

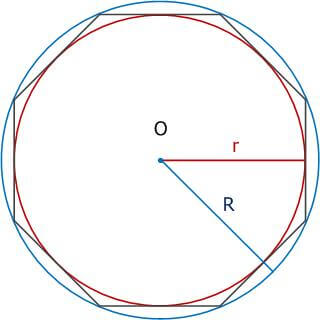
Рис. 7. Правильный восьмиугольник

Как найти площадь неправильной фигуры | Сделай все сам

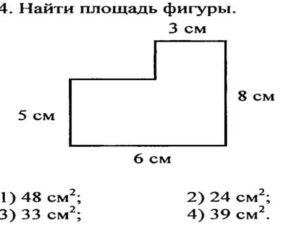
В школьном курсе геометрии ученики в основном считают площади положительных многоугольников. Между тем, для решения множества фактических задач неоднократно доводится иметь дело с неправильными геометрическими фигурами.

С этой задачей человек сталкивается и при определении размеров дачного участка либо придомовой территории, и при расчете числа ткани для шитья, и еще во многих случаях.

Высчитать площадь неправильной фигуры дозволено несколькими методами.

Вам понадобится

• – неправильная геометрическая фигура;
• – измерительные инструменты;
• – прозрачный пластик;
• – линейка;
• – угольник;
• – шариковая ручка.

Инструкция

1. Разглядите геометрическую фигуру и определите, какие ее параметры вам вестимы. Это могут быть длины сторон либо углы. В зависимости от заданных параметров и выберите метод определения площади. Скажем, поделите ее на несколько фигур, формулы вычисления площади которых вы знаете.

Один из самых распространенных способов — провести диагонали из одного угла ко каждым остальным вершинам. В этом случае вам необходимо знать формулу вычисления площади произвольного треугольника. Но никто не воспрещает поделить заданную фигуру и на другие многоугольники.

Скажем, при расчете площади пола в комнате с нишей комфортнее поделить неправильную фигуру на два прямоугольника либо квадрата.

2. Для определения площади не слишком огромный детали дозволено воспользуйтесь палеткой. Ее дозволено сделать самому. Отрежьте прямоугольный кусок всякого прозрачного пластика.

Поделите его на квадраты, площадь которых вам вестима — скажем, 1х1 либо 0,5х0,5 см. Линейка и угольник обязаны быть точными. Наложите палетку на деталь. Сосчитайте полные квадратики, после этого — неполные.

Роль палетки будет исполнять сетка из квадратов со стороной 1х1 м, начерченная на земле либо подмеченная колышками с протянутыми между ними шнурами. Дозволено ограничиться и разметкой территории на полосы. .

3. С большими площадями дозволено поступить и напротив. Возьмите максимально точный план участка либо придомовой территории. Определите масштаб. Воспользуйтесь одним из предложенных методов. После этого полученное число квадратных сантиметров переведите в надобный масштаб.

Перед тем как начинать ремонт пола в доме, нужно узнать всеобщую площадь , дабы верно рассчитать число материала. Несложная, казалось бы, задача на деле может вызвать много сложностей. Дабы положительно обнаружить площадьпола , вам нужно знать некоторые нюансы измерительной науки.

Вам понадобится

• – рулетка;
• – электронный дальномер;
• – лист бумаги и карандаш;
• – калькулятор.

Правильный восьмиугольник в природе, технике и культуре:

В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного правильного восьмиугольника.

Форма правильного восьмиугольника часто используются в изобразительном искусстве, архитектуре. Например, Собор Святого Георгия (Аддис-Абеба, Эфиопия), Купол Скалы (Иерусалим, Израиль), башня Ветров (Афины, Греция), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий (Флоренция, Италия), Ахенский собор (Ахен, Германия), Капелла Карла Великого (Ахен, Германия).

Примечание:  Фото https://www.pexels.com, https://pixabay.com

Найти что-нибудь еще?

карта сайта

Коэффициент востребованности
2 900

Какие их виды существуют?

Многоугольник, у которого больше четырех углов, может быть выпуклым или вогнутым. Отличие последнего в том, что некоторые его вершины могут лежать по разные стороны от прямой, проведенной через произвольную сторону многоугольника. В выпуклом всегда все вершины лежат с одной стороны от такой прямой.

В школьном курсе геометрии большая часть времени уделяется именно выпуклым фигурам. Поэтому в задачах требуется узнать площадь выпуклого многоугольника. Тогда существует формула через радиус описанной окружности, которая позволяет найти искомую величину для любой фигуры. В других случаях однозначного решения не существует. Для треугольника формула одна, а для квадрата или трапеции совершенно другие. В ситуациях, когда фигура неправильная или вершин очень много, принято разделять их на простые и знакомые.

Восьмиугольник, выпуклый и невыпуклый восьмиугольник:

Восьмиугольник – это многоугольник с восемью углами.

Восьмиугольник – это многоугольник, общее количество углов (вершин) которого равно восьми.

Восьмиугольник может быть выпуклым и невыпуклым.

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.

Соответственно выпуклый восьмиугольник – это восьмиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Рис. 1. Выпуклый восьмиугольник

Рис. 2. Невыпуклый восьмиугольник

Сумма внутренних углов любого выпуклого восьмиугольника равна 1080°.

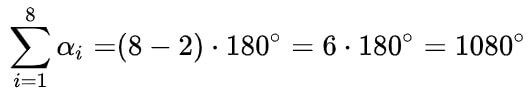
Площадь правильного пятиугольника, зная его радиус

В радио правильного многоугольника — это отрезок, идущий от центра до одной из его вершин. Он соответствует радиусу описанной окружности, как показано на следующем рисунке:

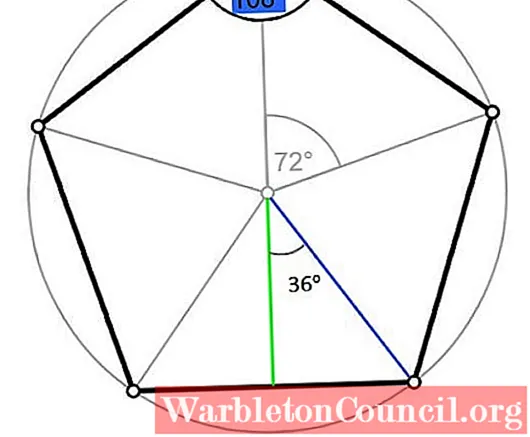
Пусть R — мера указанного радиуса, которая совпадает с гипотенузой прямоугольного треугольника, выделенного синим цветом на предыдущем рисунке. По тригонометрии:

cos 36º = cos (π / 5) = L_К ÷ R

Y

sin 36º = sin (π / 5) = (a / 2) ÷ R

Таким образом:

А = P x L_К / 2 = 5р. sin (π / 5) x R. cos (π / 5) = 5R2 [sin (π / 5) x cos (π / 5)]

Используя формулу двойного угла:

грех (2θ) = 2 греха θ. cos θ

У нас это:

[sin (π / 5) x cos (π / 5)] = (1/2) sin 72º

Итак, подставив это значение, мы получим следующую формулу для площади правильного пятиугольника:

А = (5/2) R2.sen 72º

Правильный восьмиугольник (понятие и определение):

Правильный восьмиугольник (октагон) – это правильный многоугольник с восемью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

Правильный восьмиугольник – это восьмиугольник, у которого все стороны равны, а все внутренние углы равны 135°.

Рис. 3. Правильный восьмиугольник

Правильный восьмиугольник имеет 8 сторон, 8 углов и 8 вершин.

Углы правильного восьмиугольника образуют восемь равнобедренных треугольников.

Правильный восьмиугольник можно построить с помощью циркуля и линейки: проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.

3. Площадь через квадрат

Площадь можно также вычислить как усечение квадрата

где A — ширина восьмиугольника вторая меньшая диагональ, а a — длина его стороны. Это легко показать, если провести через противоположные стороны прямые, что даст квадрат. Легко показать, что угловые треугольники равнобедренные с основанием, равным a. Если их сложить как на рисунке, получится квадрат со стороной a.

Если задана сторона a, то длина A равна

Тогда площадь равна:

Площадь через A ширину восьмиугольника

Ещё одна простая формула площади:

Часто значение A известно, в то время как величину стороны a следует найти, как, например, при отрезании от квадратного куска материала углов с целью получения правильного восьмиугольника. Из формул выше имеем

Геометрия многоугольников

В целом такая геометрическая фигура может иметь абсолютно любой вид. К примеру, символы звезды и компаса, полигон для моделирования или грань шестеренки — многоугольники. Многоугольные фигуры разделяются на две группы:

• невыпуклые, которые имеют любую причудливую форму с возможными самопересечениями (самый очевидный пример — звезда);
• выпуклые, все точки которых находятся по одну сторону от прямой, проведенной через две соседние вершины (квадрат, треугольник).

Выпуклый полигон, у которого все углы равны и все стороны равны, считается правильным и имеет собственное название. К примеру, правильный пятиугольник называется пентагон, шести — гексагон, восьмиугольник — октагон, десятиугольник — декагон, одиннадцатиугольник — гендекагон, двенадцати — додекагон. Любой правильный многоугольник имеет свою вписанную и описанную окружность. При этом круг также можно представить как правильный полигон, который имеет бесконечное количество углов.

2. Формулы расчёта параметров правильного восьмиугольника

Пример:

• k — константа, равная 1 + 2 {\displaystyle 1+{\sqrt {2}}} ≈ 2.414213562373095
• R — радиус описанной окружности
• S — площадь восьмиугольника
• r — радиус вписанной окружности
• t — длина стороны восьмиугольника

Так как правильный восьмиугольник можно получить соответствующим отсечением углов квадрата со стороной k t {\displaystyle kt}, радиус вписанной окружности, радиус описанной окружности и площадь правильного восьмиугольника можно вычислить и без использования тригонометрических функций:

Радиус вписанной окружности правильного восьмиугольника

Радиус описанной окружности правильного восьмиугольника

Площадь правильного восьмиугольника

Через сторону восьмиугольника

Через радиус описанной окружности

Площадь многоугольника

Площадь геометрической фигуры — это характеристика плоского объекта, которая показывает его размер. Площадь невыпуклых многоугольников находится путем разбиения фигуры на более мелкие составляющие, обычно треугольники или квадраты. Наш онлайн-калькулятор позволяет вычислять площадь только правильных многоугольников, которая определяется общей формулой:

S = n/4 × a^2 × ctg(pi/n),

где n — количество сторон фигуры, a — длина стороны.

Подставляя вместо n количество сторон фигуры можно получить формулу для определения площади любого правильного полигона, которая будет представлять собой площадь квадрата a^2, умноженного на определенный коэффициент. Интересно, что при увеличении количества углов этот коэффициент также будет увеличиваться, к примеру, для пентагона — 1,72, а гексагона — 2,59.

Так как около любого правильного полигона можно описать окружность или вписать ее в него, мы можем использовать соответствующие радиусы для вычисления площадей многоугольников. Сторона и радиус описанной окружности для любого полигона соотносятся как:

a = R × 2 sin (pi/n),

где R – радиус описанной окружности, n – количество сторон геометрической фигуры.

Для вписанной в полигон окружности соотношение немного изменяется и выглядит как:

a = r × 2 tg (pi/n),

где r – радиус вписанной окружности.

Таким образом, для определения площади любого правильного полигона вам понадобится указать количество сторон n и любой параметр на выбор:

• длина стороны a;
• радиус вписанной окружности r;
• радиус описанной окружности R.

Рассмотрим пару примеров для нахождения площади любого многоугольника.

4. Симметрия

Правильный восьмиугольник имеет группу симметрии Dih 8 порядка 16. Имеется 3 диэдральные подгруппы — Dih 4, Dih 2 и Dih 1, а также 4 циклические подгруппы — Z 8, Z 4, Z 2 и Z 1. Последняя подгруппа подразумевает отсутствие симметрии.

Правильный восьмиугольник имеет 11 различных симметрий. Джон Конвей обозначил полную симметрию как r16. Диэдральные симметрии делятся на симметрии, проходящие через вершины обозначены как d — от diagonal, или через рёбра обозначены как p — от perpendiculars. Циклические симметрии в среднем столбце обозначены буквой g и для них указан порядок группы вращения. Полная симметрия правильного восьмиугольника обозначена как r16 а отсутствие — как a1.

На рисунке слева показаны типы симметрий восьмиугольников. Наиболее общие симметрии восьмиугольников — p8, равноугольный восьмиугольник, построенный четырьмя зеркалами и имеющий перемежающиеся длинные короткие стороны, и d8, изотоксальный восьмиугольник, имеющий рёбра равной длины, но вершины имеют два разных внутренних угла. Эти две формы являются двойственным друг другу и имеют порядок, равный половине симметрии правильного восьмиугольника.

Как найти площадь пятиугольника | Сделай все сам

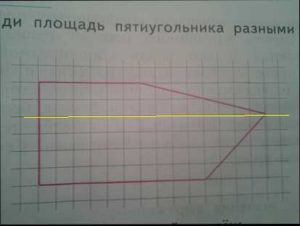
Это достаточно простая задача школьного курса. Для ее решения довольно знать несколько простейших математических формул, которые являются основополагающими в геометрии. Также потребуется знание логически думать и считать на калькуляторе.

Вам понадобится

• – минимальные данные, нужные для решения задачи, а именно длина всякой стороны и диагонали пятиугольника;
• – калькулятор;
• – ручка;
• – лист бумаги.

Инструкция

1. Наблюдательно прочитайте условие поставленной задачи. Руководствуясь им, нарисуйте на листе бумаги полагаемый пятиугольник.

2. Обозначьте длину всей из его сторон.

3. Проведите в пятиугольнике две диагонали. Обозначьте длину всякой диагонали.

4

Обратите внимание на то, что получилось в итоге проведения диагоналей, и вы увидите, что они разбивают пятиугольник на три разных между собой треугольника

5. Из вершины всего треугольника проведите высоту к его основанию.

6. Измерьте длину высоты опущенной на основание для всего треугольника.

7. Определите площади всех 3 треугольников по формуле, приведенной ниже:S = ? ? H ? a,где S – вычисляемая площадь треугольника;H – высота всего треугольника;a – длина основания треугольника.

8. Вычислите площадьпятиугольника , сложив площади этих 3 треугольников.

Когда речь заходит о вычислении площади, то почаще каждого имеется в виду не поверхность какой-нибудь трудной пространственной конфигурации, а участок ограниченной периметром двухмерной плоскости.

Если такая поверхность имеет правда бы примерно положительную форму, то для расчетов с заданной степенью точности дозволено задействовать знаменитые формулы вычисления площади соответствующих геометрических фигур.

Заключение

Правильный полигон — это не только экзотический додекагон, но и квадрат или равносторонний треугольник, а значит, такую фигуру вы обязательно встретите не только в школьных задачах, но и в быту, на работе и в реальной повседневности. Используйте наш калькулятор для определения площадей любых правильных многоугольников.

Вычисление площади многоугольникаГородская научно-практическая конференция юных исследователей
«Будущее Петрозаводска»
Вычисление площади
многоугольника
Качановская Алина Игоревна
9Б класс, г. Петрозаводск.
учитель математики
МОУ «Гимназия №30 имени Музалева Д.Н.»